|
Feature: Air To Air Gunnery - Theory and Application, Part Two
Back To Page 2
Stadiametric ranging
Stadiametric ranging uses the relationship of small angles and the arcs they
subtend over a given distance. Whew!! I hope you are still with
me!! Here is the basic idea.
We all are familiar with how we use clock code to
define a position around our aircraft. Each one hour of the clock
represents an angle of 30 degrees. We can use angles to estimate range, as
well as position. We begin by focusing on a very small angle…one degree.
I ’ll now draw a figure that shows how this small angle can be used to compute
range. The point of origin for this angle will be our gunsight, and the
lines of the angle will be projected along the sight line. Sometimes a
picture is easier to understand.
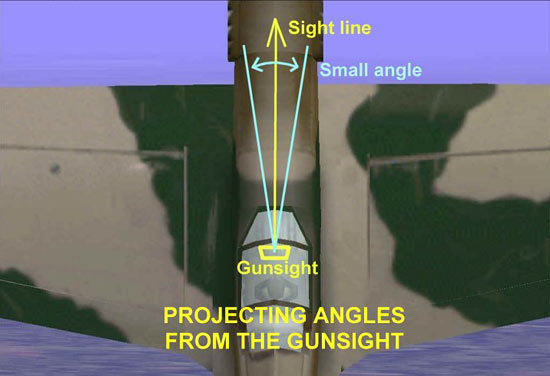
Now, we go to the math part. The distance
between the two lines of the angle is known as the arc that the angle
subtends. Fighter pilot instructors will say it this way; "The angle
‘x’ subtends an arc of ‘y’ feet at a distance of ‘z’
feet." Notice the unit of measurement for distance is feet. The
unit of measurement for angles is NOT degrees…it is a value known as a ‘mil.’
There are about 17 mils in one degree…so a mil is just a very small
angle. This is the definition of a mil:
A mil is an angle that subtends one foot at 1000
feet range. The arc size versus
range relationship is linear, therefore, one mil = one foot at 1000 feet, two
feet at 2000 feet range, and so on. Similarly, if one mil = one foot at
1000 feet, then 10 mils equals 10 feet at 1000 feet range, 20 feet at 2000 feet
range and so on.
Let’s show a practical example of this
concept. Go out to your car and then pace off exactly 50 feet and mark
that spot. Now, get a piece of glass and look through it at your
car. Draw a line on the glass equal to how long your car appears.
Next, draw a circle on that piece of glass with a diameter equal to that
line. You now have a tool to find out how far 50 feet is using your car as
a reference. Just walk towards your car looking through the glass.
When the car length matches the diameter of the circle, you are at 50 feet!!
Now we take this idea and apply it to a
gunsight. Let’s draw a circle on a piece of glass and say its diameter
is a certain number of mils wide. If we were to hold that circle up in
front of our eye and look through it, then the circle could be used to show what
a certain distance looks like at a given range. For example, if we said
that the circle had a diameter of 50 mils, then the circle would span a distance
of 50 feet at 1000 feet range.
You know where I’m going with this…right?!!
Now, we’ll think of that circle as our gunsight reticle. We know the mil
value of the gunsight reticle…50 mils in this example. The two remaining
variables are range and arc distance. Let’s change the name ‘arc
distance’ to ‘wingspan.. We now have a simple mathematical situation
where we can solve the problem of determining target range. Here’s how.
Pick a target…say a Su-27. Its wingspan is a known value…approximately
50 feet.
Let’s put ourselves at the Flanker’s six and
compare its wingspan to our 50 mil reticle. Picture in your mind the
wingtips just touching the edges of the reticle. The range computation is
"The 50 foot wingspan is 50 mils in size…therefore the range is 1000
feet." Now, let’s pull the power back and increase our distance
behind the Flanker. When we look at the Flanker in the reticle now, its
wingspan looks to be about one fourth of the reticle diameter, or about 12
mils. What is the new range? Divide the observed wingspan size in
mils into the known wingspan size in feet…forget about the decimal
points!! 12 into 50 equals about 4…so the range is about 4000
feet. The next figure explains the process.
Some might ask why am I going through all this
hoopla. The answer is simple. Effective use of the gun requires a
pilot to estimate range quickly and correctly. Gunsight reticle and funnel
displays are made to be a certain size to help the pilot accomplish this.
Go
To Page 4
Click
here to go to top of this page.
|
